Calculating the Pearson product-moment correlation coefficient

The Pearson product-moment correlation coefficient (PMCC) is a quantity between -1.0 and 1.0 that estimates the strength of the linear relationship between two random variables.

The PMCC in its usual form is somewhat cumbersome to calculate. Using simple algebra, I have rearranged it to form an expression that should have better numerical stability and require fewer calculations.

Disclaimer: This page is primarily for my own reference. I am a programmer without formal training in statistics, and I don't even feel like I know what I'm doing. There are probably a ton of assumptions that I am unwittingly making, I am almost certainly misusing the terminology, and I could simply be flat-out wrong here. My apologies to statisticians and to people like Zed Shaw who have a far greater understanding of this stuff than I do. If you blindly trust this page while building something important---even after what I just told you---then the blame is all yours. Use your brain. Don't believe everything you read. This is not even a very interesting article: It's mostly just algebra. Don't read this page; It's a waste of your time.

On a more serious note: In an attempt to make this article less cringe-worthy, I made an effort to find the original peer-reviewed article(s) where the Pearson correlation might be defined precisely, but nothing I read cited primary references (MathWorld just cited textbooks, for example) and I don't have the money to buy expensive journal articles for every little web page I write. After searching for most of a day, I finally gave up in frustration and decided to post this article anyway, flaws and all. If this article makes you cringe, please consider doing something to advance the principle of open access.

The Math

Product-Moment Correlation Coefficient (PMCC)

Imagine we have two populations X and Y. Then ρ_X,Y represents the product-moment coefficient of correlation between them.

Various websites and textbooks describe the correlation coefficient in several equivalent ways:

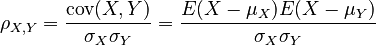
As the ratio between the covariance of X and Y and the product of their standard deviations:: $\rho_{X,Y} = \frac{\textrm{cov}(X, Y)}{\sigma_X \sigma_Y} = \frac{E(X - \mu_X) E(X - \mu_Y)}{\sigma_X \sigma_Y}$
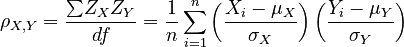
As the sum of the products of each pair of standard scores of the X and Y values, all divided by the number of degrees of freedom:: $\rho_{X,Y} = \frac{{\sum} Z_X Z_Y}{df} = \frac{1}{n} \sum_{i=1}^n \left(\frac{X_i - \mu_X}{\sigma_X}\right) \left(\frac{Y_i - \mu_Y}{\sigma_Y}\right)$

We often can't work with populations directly, so we can't determine the exact value of ρ_X,Y. However, we can estimate it by selecting a random sample of (x,y) pairs. This estimate is often labelled r. Since we can use the same formula for either case, I call the general formula PMCC(X,Y).

Definitions

Let PMCC(X,Y) be the Pearson product-moment correlation coefficient of two n-dimensional vectors X = {X₁,X₂,...,X_n} and Y = {Y₁,Y₂,...,Y_n}.

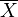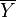Let $\overline{X}$ and $\overline{Y}$ be the arithmetic means of the elements in X and Y, respectively.

Let s_X and s_Y be the standard deviations of X and Y, respectively.

Then, the following relations apply. Note how we define N in order to avoid having to do two separate analyses for population and sample data:

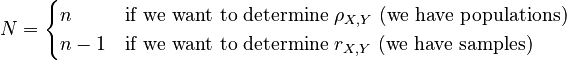$N = \begin{cases} n & \textrm{if~we~want~to~determine~}\rho_{X,Y}\textrm{~(we~have~populations)}\\ n-1 & \textrm{if~we~want~to~determine~}r_{X,Y}\textrm{~(we~have~samples)} \end{cases}$
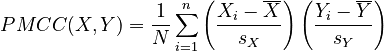$PMCC(X,Y) = \frac{1}{N} \sum_{i=1}^n \left(\frac{X_i - \overline{X}}{s_X}\right) \left(\frac{Y_i - \overline{Y}}{s_Y}\right)$
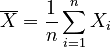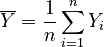$\overline{X} = \frac{1}{n} \sum_{i=1}^n {X_i}$	,	$\overline{Y} = \frac{1}{n} \sum_{i=1}^n {Y_i}$
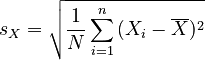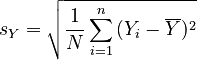$s_X = \sqrt{ \frac{1}{N} \sum_{i=1}^n {(X_i - \overline{X})^2} }$	,	$s_Y = \sqrt{ \frac{1}{N} \sum_{i=1}^n {(Y_i - \overline{Y})^2} }$

Simple sums

Given the vectors X and Y, there are a few things we can calculate right away:

The sums of all the elements in each vector:
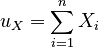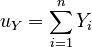$u_X = \sum_{i=1}^n X_i$	,	$u_Y = \sum_{i=1}^n Y_i$
The squares of the sums of all the elements in each vector:
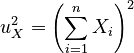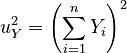$u_X^2 = \left( \sum_{i=1}^n X_i \right)^2$	,	$u_Y^2 = \left( \sum_{i=1}^n Y_i \right)^2$
The sums of the squares of all the elements in each vector:
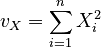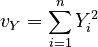$v_X = \sum_{i=1}^n X_i^2$	,	$v_Y = \sum_{i=1}^n Y_i^2$
The sum of the products of the corresponding elements from each vector:
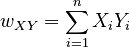$w_{XY} = \sum_{i=1}^n X_i Y_i$

Arithmetic means

We can now reduce the arithmetic means in terms of our previous calculations:

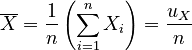
$\overline{X} = \frac{1}{n} \left( \sum_{i=1}^n X_i \right) = \frac{u_X}{n}$

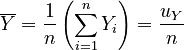
$\overline{Y} = \frac{1}{n} \left( \sum_{i=1}^n Y_i \right) = \frac{u_Y}{n}$

Standard deviations

To simplify the standard deviations, we first reduce the squares of the deviations:

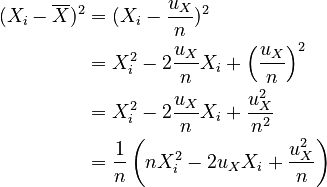
$\begin{align} (X_i - \overline{X})^2 &= (X_i - \frac{u_X}{n})^2 \\ &= X_i^2 - 2\frac{u_X}{n} X_i + \left(\frac{u_X}{n}\right)^2\\ &= X_i^2 - 2\frac{u_X}{n} X_i + \frac{u_X^2}{n^2}\\ &= \frac{1}{n} \left( n X_i^2 - 2 u_X X_i + \frac{u_X^2}{n} \right) \end{align}$

Then, we simplify the variance:

$\begin{align} s_X^2 &= \frac{1}{N} \sum_{i=1}^n (X_i - \overline{X})^2 \\ &= \frac{1}{N} \sum_{i=1}^n \left[ \frac{1}{n} \left( n X_i^2 - 2 u_X X_i + \frac{u_X^2}{n} \right) \right] \\ &= \frac{1}{N} \frac{1}{n} \sum_{i=1}^n \left( n X_i^2 - 2 u_X X_i + \frac{u_X^2}{n} \right) \\ &= \frac{1}{N} \frac{1}{n} \left[ \left( \sum_{i=1}^n n X_i^2 \right) - \left( \sum_{i=1}^n 2 u_X X_i \right) + \left( \sum_{i=1}^n \frac{u_X^2}{n} \right) \right] \\ &= \frac{1}{N} \frac{1}{n} \left[ (n) \left( \sum_{i=1}^n X_i^2 \right) - (2 u_X) \left( \sum_{i=1}^n X_i \right) + \left( \frac{u_X^2}{n} \right) \left( \sum_{i=1}^n 1 \right) \right] \\ &= \frac{1}{N} \frac{1}{n} \left[ (n) (v_X) - (2 u_X) (u_X) + \left( \frac{u_X^2}{n} \right) (n) \right] \\ &= \frac{1}{N} \frac{1}{n} \left( n v_X - 2 u_X^2 + u_X^2 \right) \\ &= \frac{1}{n N} \left( n v_X - u_X^2 \right) \end{align}$

Therefore, the reduced standard deviations are:

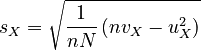$s_X = \sqrt{ \frac{1}{n N} \left( n v_X - u_X^2 \right) }$

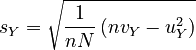$s_Y = \sqrt{ \frac{1}{n N} \left( n v_Y - u_Y^2 \right) }$

Reducing the PMCC formula, Part 1

Recall the PMCC formula:

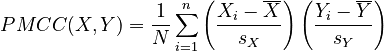$PMCC(X,Y) = \frac{1}{N} \sum_{i=1}^n \left(\frac{X_i - \overline{X}}{s_X}\right) \left(\frac{Y_i - \overline{Y}}{s_Y}\right)$

and the results we derived:

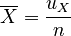
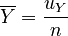
$\overline{X} = \frac{u_X}{n}$	,	$\overline{Y} = \frac{u_Y}{n}$
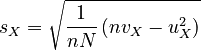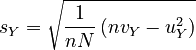$s_X = \sqrt{ \frac{1}{n N} \left( n v_X - u_X^2 \right) }$	,	$s_Y = \sqrt{ \frac{1}{n N} \left( n v_Y - u_Y^2 \right) }$

Performing substitution, we get:

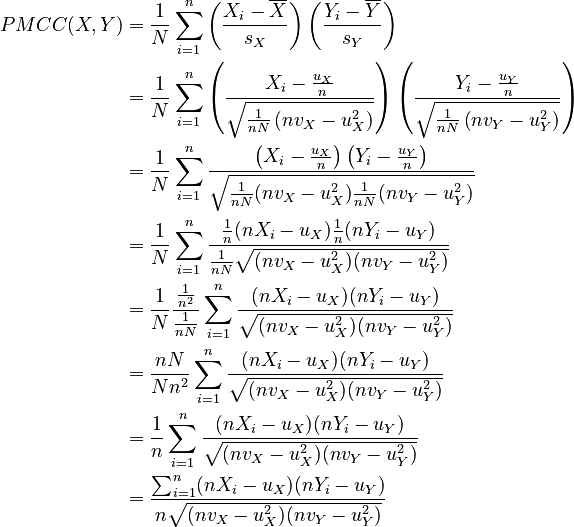
$\begin{align} PMCC(X,Y) &= \frac{1}{N} \sum_{i=1}^n \left(\frac{X_i - \overline{X}}{s_X}\right) \left(\frac{Y_i - \overline{Y}}{s_Y}\right)\\ &= \frac{1}{N} \sum_{i=1}^n \left(\frac{X_i - \frac{u_X}{n}}{\sqrt{ \frac{1}{n N} \left( n v_X - u_X^2 \right) }}\right) \left(\frac{Y_i - \frac{u_Y}{n}}{\sqrt{ \frac{1}{n N} \left( n v_Y - u_Y^2 \right) }}\right)\\ &= \frac{1}{N} \sum_{i=1}^n \frac{ \left(X_i - \frac{u_X}{n}\right) \left(Y_i - \frac{u_Y}{n}\right) }{ \sqrt{ \frac{1}{n N} ( n v_X - u_X^2 ) \frac{1}{n N} ( n v_Y - u_Y^2 ) } }\\ &= \frac{1}{N} \sum_{i=1}^n \frac{ \frac{1}{n} ( n X_i - u_X ) \frac{1}{n} ( n Y_i - u_Y ) }{ \frac{1}{n N} \sqrt{ ( n v_X - u_X^2 ) ( n v_Y - u_Y^2 ) } }\\ &= \frac{1}{N} \frac{\frac{1}{n^2}}{\frac{1}{n N}} \sum_{i=1}^n \frac{ ( n X_i - u_X ) ( n Y_i - u_Y ) }{ \sqrt{ ( n v_X - u_X^2 ) ( n v_Y - u_Y^2 ) } }\\ &= \frac{n N}{N n^2} \sum_{i=1}^n \frac{ ( n X_i - u_X ) ( n Y_i - u_Y ) }{ \sqrt{ ( n v_X - u_X^2 ) ( n v_Y - u_Y^2 ) } }\\ &= \frac{1}{n} \sum_{i=1}^n \frac{ ( n X_i - u_X ) ( n Y_i - u_Y ) }{ \sqrt{ ( n v_X - u_X^2 ) ( n v_Y - u_Y^2 ) } }\\ &= \frac{ \sum_{i=1}^n ( n X_i - u_X ) ( n Y_i - u_Y ) }{ n \sqrt{ ( n v_X - u_X^2 ) ( n v_Y - u_Y^2 ) } }\\ \end{align}$

Notice how the formula no longer depends on whether the data is from a population or from a sample.

Reducing the PMCC formula, Part 2

Let's reduce the summation from the previous section:

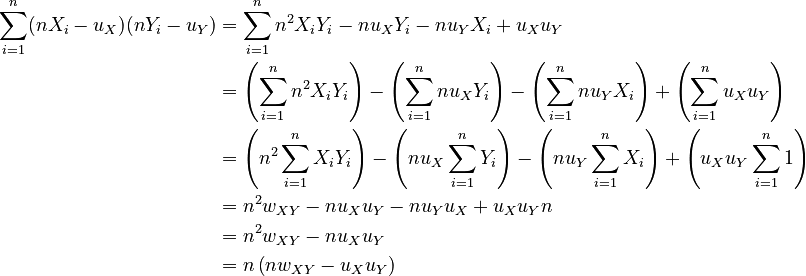
$\begin{align} \sum_{i=1}^n ( n X_i - u_X ) ( n Y_i - u_Y ) &= \sum_{i=1}^n n^2 X_i Y_i - n u_X Y_i - n u_Y X_i + u_X u_Y\\ &= \left( \sum_{i=1}^n n^2 X_i Y_i \right) - \left( \sum_{i=1}^n n u_X Y_i \right) - \left( \sum_{i=1}^n n u_Y X_i \right) + \left( \sum_{i=1}^n u_X u_Y \right) \\ &= \left( n^2 \sum_{i=1}^n X_i Y_i \right) - \left( n u_X \sum_{i=1}^n Y_i \right) - \left( n u_Y \sum_{i=1}^n X_i \right) + \left( u_X u_Y \sum_{i=1}^n 1 \right) \\ &= n^2 w_{XY} - n u_X u_Y - n u_Y u_X + u_X u_Y n \\ &= n^2 w_{XY} - n u_X u_Y \\ &= n \left( n w_{XY} - u_X u_Y \right) \\ \end{align}$

Substituting, we get:

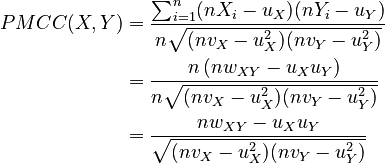
$\begin{align} PMCC(X,Y) &= \frac{ \sum_{i=1}^n ( n X_i - u_X ) ( n Y_i - u_Y ) }{ n \sqrt{ ( n v_X - u_X^2 ) ( n v_Y - u_Y^2 ) } }\\ &= \frac{ n \left( n w_{XY} - u_X u_Y \right) }{ n \sqrt{ ( n v_X - u_X^2 ) ( n v_Y - u_Y^2 ) } } \\ &= \frac{ n w_{XY} - u_X u_Y }{ \sqrt{ ( n v_X - u_X^2 ) ( n v_Y - u_Y^2 ) } } \\ \end{align}$

Conclusion

Given two populations or samples X = {X₁,X₂,...,X_n} and Y = {Y₁,Y₂,...,Y_n} (and subject to some assumptions about the distributions of the data), the Pearson product-moment correlation coefficient of the two is given by:

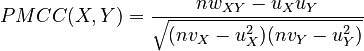
$PMCC(X,Y) = \frac{ n w_{XY} - u_X u_Y }{ \sqrt{ ( n v_X - u_X^2 ) ( n v_Y - u_Y^2 ) } }$

where the following variables are defined:

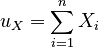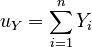$u_X = \sum_{i=1}^n X_i$	,	$u_Y = \sum_{i=1}^n Y_i$
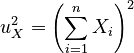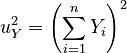$u_X^2 = \left( \sum_{i=1}^n X_i \right)^2$	,	$u_Y^2 = \left( \sum_{i=1}^n Y_i \right)^2$
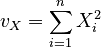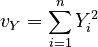$v_X = \sum_{i=1}^n X_i^2$	,	$v_Y = \sum_{i=1}^n Y_i^2$
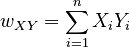$w_{XY} = \sum_{i=1}^n X_i Y_i$

Alternatively, we can use the expanded form (which is obtained by applying the previous substitutions):

$PMCC(X,Y) = \frac{ n \left( \sum_{i=1}^n X_i Y_i \right) - \left( \sum_{i=1}^n X_i \right) \left( \sum_{i=1}^n Y_i \right) }{ \sqrt{ \left[ n \left( \sum_{i=1}^n X_i^2 \right) - \left( \sum_{i=1}^n X_i \right)^2 \right] \left[ n \left( \sum_{i=1}^n Y_i^2 \right) - \left( \sum_{i=1}^n Y_i \right)^2 \right] } }$

Implementation issues

Computing sums of many terms

When computing the sum of several floating-point values that vary widely, you can obtain a better approximation (less round-off error) by sorting the terms in ascending order before adding them together. That way, the smaller numbers will be added together before being added to larger numbers, rather than being immediately truncated. The Wikipedia article on numerical stability has a bit more information about this.